Introduction
Implementing a pathways approach for college students is on the rise as higher education institutions work to combat the persistent problem of low student completion. In general, a pathways approach defines an effective and intentional student experience based on data and best practice. For example, the American Association of Community Colleges (AACC) Guided Pathways Project has led many colleges to seek better definition along a student’s academic trajectory from enrollment to postsecondary completion.
The same principle of defining an effective and intentional pathway can be applied to mathematics. Without clearly defined mathematics pathways, mathematics can serve as a barrier to student completion and success. This barrier often occurs in four ways: 1) students flounder in developmental mathematics courses, 2) students do not pass their required mathematics courses, 3) students delay enrolling in mathematics courses, and 4) students enroll in mathematics courses that do not prepare them for their selected programs of study.
When used effectively, mathematics pathways address these barriers. Evidence suggests that students, including those needing developmental support, can succeed in college-level mathematics courses with appropriate assistance delivered through a one-semester, corequisite model. Regardless of the model, student success relies on pathways that incorporate rigorous and relevant mathematics aligned to programs of study and that are informed by major professional organizations.
Visit the Dana Center Mathematics Pathways (DCMP) resource site to learn about its history, vision, and four principles that guide the DCMP work.
How to Use This Guide
This guide is designed for faculty and staff at two-year and four-year institutions that are implementing and scaling mathematics pathways based on DCMP principles. It offers a blueprint comprising four stages that guide different stakeholder groups in planning for implementation of mathematics pathways at their institutions and in monitoring efforts for continuous improvement.
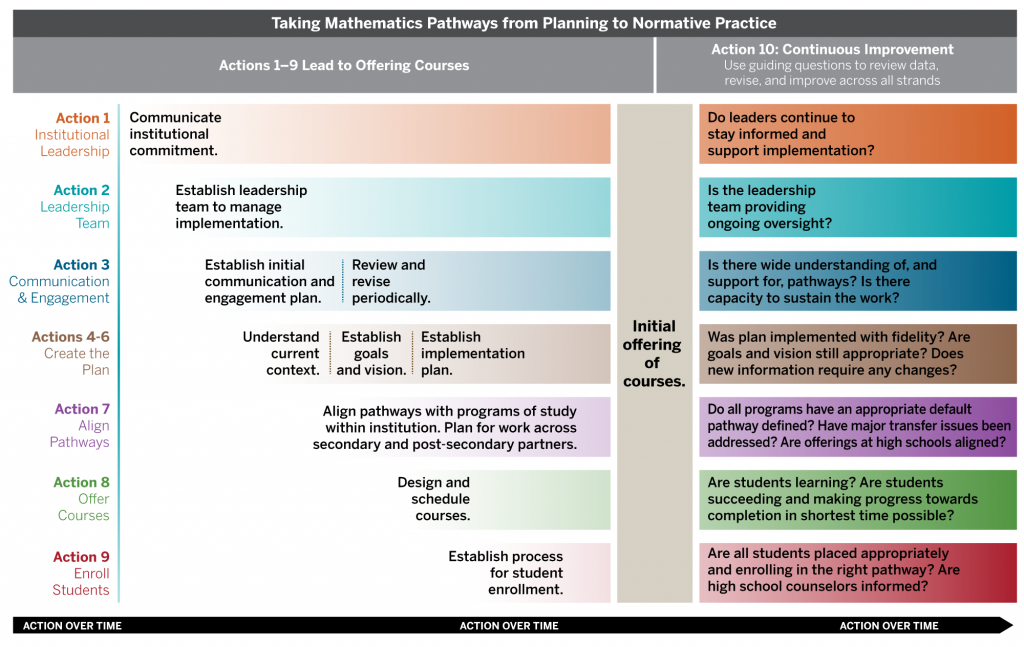
The graphic below shows that these stages do not exist in isolation nor is the implementation process merely linear. Stages may overlap, and institutional circumstances may necessitate additional actions to enact a stage. Further, some actions (i.e., Essential Actions 4, 5, and 8) end for institutions after certain steps and activities, whereas other actions (i.e., Essential Actions 1, 2, 3, 6, 7, 9, and 10) are ongoing until normative practice is established.
This online guide offers the following features:
- Stages of implementation – necessary operations required for successful mathematics pathways
- Essential actions – key actions that must be completed to realize the stage of implementation
- Steps to fulfill actions – activities to achieve the action
- Downloadable resources – tools and information to fulfill each action
We recommend that institutional leadership teams read this guide in its entirety before beginning the implementation process. We also suggest teams review the Learn About pages of the DCMP resource site on emerging issues, implementation stories, and role-specific tools that can guide their own efforts. By providing an email address at the top left of the page, a user is able to save their progress, so that each time a user revisits the guide at a later date, progress can be continued from the last visit.
Stages of Implementation
The Dana Center recommends a four-stage process to implement mathematics pathways:
- Getting Started (Essential Actions 1-3) – Leaders identify need, make commitment, and prepare to engage stakeholders through a leadership team.
- Planning (Essential Actions 4-7) – Cross-functional leadership team collects and reviews data to define the problem and establish goals.
- Implementing (Essential Actions 8-9) – Working groups and individuals follow the implementation plan under oversight of leadership team.
- Continuous Improvement (Essential Action 10) – Working groups and individuals use data-informed evidence to assess implementation progress and learn from changes to scale mathematics pathways.
This process involves 10 essential actions, which are outlined in the graphic below.